美国数学大联盟竞赛自1977年创办,至今已有近50年的历史,是美国及北美地区最具影响力的中小学数学赛事之一。该赛事不仅注重考察学生的数学知识和计算能力,更强调培养创造性思维、批判性思维以及解决实际问题的能力。其试题灵活生动、富有趣味性且贴近生活,旨在激发学生学习数学的兴趣,让学生理解和欣赏数学的魅力。
赛事根据学生年级分为不同组别,覆盖从小学到高中各个阶段。比赛采用循序渐进的晋级制度,主要分为三个阶段:第一阶段(初赛)、第二阶段(复赛)以及决赛和数学夏令营。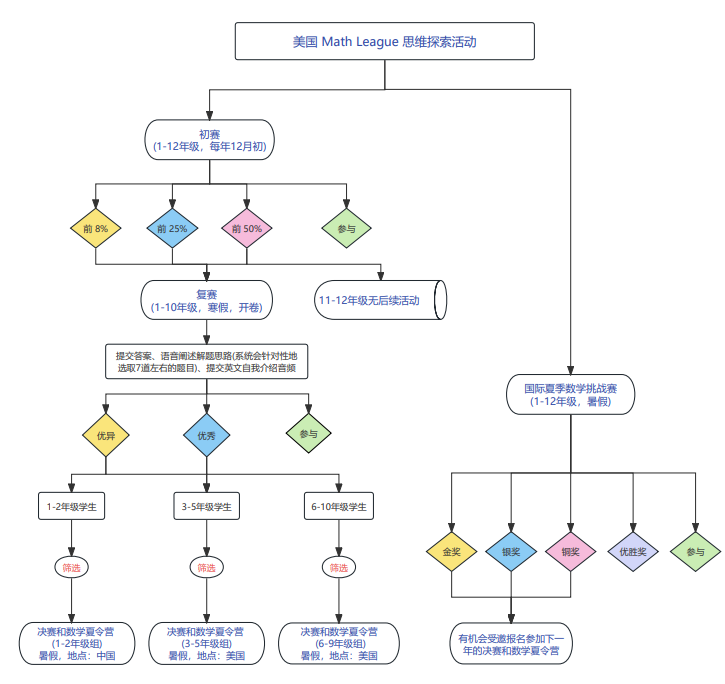
一、各环节详细竞赛内容
1. 第一阶段(初赛)
比赛形式与规则:第一阶段是所有学生均可报名参加的初始环节。比赛形式通常为在线进行(中国区)。初赛除1-2年级外为全英文,但组委会会提供在线数学常用词汇表(英汉对照),以帮助非英语母语的学生理解题意。考试期间禁止使用任何字典、计算器或参考资料。
各年级试题结构:
1-2年级:试题约为45道选择题,答题时间为45分钟。试题以图形题为主,主要考察学生的思维能力,辅以少量考察数学知识和能力的题目。
3-7年级:35道选择题或填空题,答题时间75分钟,总分为175分。
8-9年级:30道选择题的试卷,答题时间75分钟,总分150分。
10-12年级:30道选择题或填空题,共30道题,答题时间75分钟。
考察重点:本阶段试题侧重于基础数学知识的掌握,但出题方式灵活,强调趣味性和应用性,旨在激发学生兴趣。
2. 第二阶段(复赛)
参赛资格:第一阶段成绩排名前50%的3-9年级学生有资格进入第二阶段的比赛。
比赛形式与规则:第二阶段比赛采用开卷形式。学生需要先阅读一段英文撰写的数学专题材料(例如数论、几何等),然后完成若干道与该专题相关的题目,难度由浅入深。学生可以查找资料(包括互联网)或询问专家,但必须独立完成,不能与他人交流。
考察重点:本阶段的核心目标是让学生体验美式数学的探索性学习方式。它不仅考察数学能力,更着重评估学生的英语阅读理解能力、自主研究能力、创造性思维和解决实际问题的能力。
3. 第三阶段(决赛暨数学夏令营)
参赛资格与地点:复赛获得优异或者优秀证书的学⽣有资格报名参加决赛和数学夏令营。
2026年美国Math League决赛夏令营信息总览
|
年级组 |
比赛地点 |
夏令营时间(暂定) |
主要考试环节 |
备注 |
|---|---|---|---|---|
|
1-2年级组 |
亚洲(具体地点待公布) |
2026年7月(具体日期待公布) |
信息待公布 |
细节有待官方后续发布 |
|
3-5年级组 |
美国,新泽西学院(距离普林斯顿大学17公里) |
2026年7月11日 - 7月18日 |
个人决赛:个人赛、速度赛 |
采用封闭式管理,学生不可离开营地 |
|
6-10年级组 |
美国,新泽西学院(距离普林斯顿大学17公里) |
2026年7月19日 - 7月27日 |
个人决赛:个人赛、速度赛 |
采用封闭式管理,学生不可离开营地 |
比赛形式:决赛阶段的竞赛形式多样,挑战性极高,通常包含以下轮次:
个人赛:选手独立解题,每次仅获得一道题,限时7-10分钟完成,题目具有一定难度。
速度赛:要求在45分钟内完成60道相对简单但题量巨大的填空题或选择题,极度考验答题速度和准确度。
团队赛:团队成员在1-2小时内共同解决10-15道题目,考察团队协作能力。
接力赛:5名队员排成一列,依次解题,后一道题的解答需要前一道题的答案,极具趣味性和挑战性,考验团队配合和快速验证能力。
考察重点:决赛试题由Math League与顶尖大学联合命题,具有很高的挑战性,核心在于考察学生创造性地解决问题和创新思维的能力。
二、 各环节详细知识点分解
以下表格系统地梳理了Math League竞赛各年级段所涉及的核心知识点。
|
知识模块 |
详细知识点内容 |
常见考察年级 |
|---|---|---|
|
基础代数运算 |
整数、分数、小数的四则运算及性质;比例与百分比;一元一次方程及应用题;多元一次方程组;指数和根式的基本运算。 |
3-9年级为核心,高阶内容延伸至初高中 |
|
几何基础 |
平面图形(三角形、四边形等)的性质、角度、周长与面积计算(包括圆和多边形);简单立体图形(立方体、圆柱)的体积和表面积;基础几何变换。 |
全年级覆盖,随年级升高而加深 |
|
数论初步 |
奇偶性分析;整除规则(如被2, 3, 5, 9整除的特征);质数与合数的判断与性质;最大公约数(GCD)与最小公倍数(LCM)的求解与应用。 |
3年级及以上,常见于逻辑推理题 |
|
组合与概率 |
基础计数原理(加法原理、乘法原理);简单的排列组合计算;古典概率模型(等可能事件概率计算)。 |
中高年级(5年级及以上) |
|
逻辑推理 |
数字谜题(如数独变体);图形或数字的模式识别与规律寻找;基于条件的真假陈述判断与逻辑推导。 |
全年级覆盖,是考察重点 |
|
函数与图表 |
一次函数的图像与性质(斜率、截距);从统计图表(柱状图、折线图)中读取信息并分析;简单的输入输出关系理解。 |
6年级及以上,特别是初高中 |
|
应用题建模 |
将实际问题(如行程问题、工程问题、购物折扣、浓度问题等)转化为数学表达式并求解,综合运用代数与几何知识。 |
全年级覆盖,是核心考察方式 |
|
创新思维题 |
开放性问题、最优策略设计、多步骤复杂逻辑链问题,旨在考察学生的创新意识和突破常规思维的能力。 |
高年级决赛阶段 |
